从DFT到FFT——快速傅立叶变换教程

发表于2022-08-19更新于2023-04-30阅读次数

一、前言

写这篇博客的起因是有一个老哥（shallow）说他学不会 FFT 。我非常奇怪，FFT 这么简单，怎么会看不懂呢？他说网上教程都是 OI 用的，说的都是多项式那一套，对我没用啊。所以我就决定写一篇教程吧，从离散傅立叶变换（DFT）入手，教你推导出 FFT 的算法。其实，DFT 到多项式的衔接只有一步而已。

我在每篇数学内容比较多的文章里都会提醒一遍：文章里会出现比较多的数学推导，它们看上去很难，但往往只是形状比较复杂，而读者对符号可能不甚了解。只要能跟着文章自己动手写一边，其实任何一个普通的高中生都很容易理解推导的过程。因此推荐大家一定要动手写一下，实在懒得动手或不方便的话也要认真看清每个符号，否则是看不懂的。

二、傅立叶变换和离散傅立叶变换

傅立叶变换，是一个改变了人们脑洞的跨时代的发明。在托勒密时期，天文学家试图用圆套圆的方式来解析行星的运动轨迹，然而傅立叶的理论告诉你：只要是个闭合曲线就能用足够多的圆拟合出来。更多有趣的例子可以在 b 站或者知乎找到，如果你不熟悉傅立叶变换，还是非常推荐你去看一下的。

已经学过信号与系统这门课的同学一定对傅立叶变换非常熟悉了，它的公式是：

F(ω)=∫−∞∞f(t)e−iωtdt.F(\omega)=\int\limits_{-\infty}^\infty f(t)e^{-i\omega t}dt.

其中 ii 为虚数单位。它的作用是把一个时域函数变化成一个频域函数，也就是写出函数在不同频率上的分量。

很显然，上面的公式适用于连续函数 f(t)f(t) ，而对于一个离散的信号序列 xnx_n ，应该用离散傅立叶变换处理它：

Xk=∑n=0N−1xne−i2πNknk=0,1,⋯ ,N−1.X_k=\sum\limits_{n=0}^{N-1}x_ne^{-i\frac{2\pi}{N}kn} \quad k=0, 1, \cdots, N-1.

这就是 DFT 的基础形式。

可以看到，对于 DFT 变换后的序列 XkX_k ，共有 N 个值，每个值都需要做 N 次计算，因此进行一次 DFT 的时间复杂度是 Θ(N2)\Theta(N^2) 的。

三、快速傅立叶变换

N2N^2 太慢了！怎么破？？

聪明的数学家们（或者计算机科学家们）发现，在这 N2N^2 次计算中，有许多操作可以进行复用。为了方便表示，我可以把 e−i2πNke^{-i\frac{2\pi}{N}k} 看成变量 x ，把 xnx_n 看成系数 ana_n ，然后把 DFT 的公式写成如下的多项式表示形式：

f(x)=a0+a1x1+a2x2+⋯+aN−1xN−1.f(x)=a_0+a_1x^1+a_2x^2+\cdots+a_{N-1}x^{N-1}.

（注意区分 xnx_n 和 xx ，它们的含义不同）

在这里，可以假设 N 是 2 的整数幂，即 N=2lN=2^l ，如果原序列的长度不是 2 的整数幂，只需要补充 0 系数使得长度为 2 的整数幂就可以了。

接着把多项式的奇数项和偶数项分开，得到

f(x)=a0+a2x2+⋯+aN−2xN−2+x(a1+a3x2+⋯+aN−1xN−2).\begin{aligned} f(x)=a_0+a_2x^2+\cdots+a_{N-2}x^{N-2} \\ +x(a_1+a_3x^2+\cdots+a_{N-1}x^{N-2}). \end{aligned}

可以发现，奇数项除掉 x 后的形式和偶数项是一样的。那么如果令

f1(x)=a0+a2x+a4x2+⋯+aN−2xN/2−1f2(x)=a1+a3x+a5x2+⋯+aN−1xN/2−1,\begin{aligned} f_1(x)=a_0+a_2x+a_4x^2+\cdots+a_{N-2}x^{N/2-1} \\ f_2(x)=a_1+a_3x+a_5x^2+\cdots+a_{N-1}x^{N/2-1}, \end{aligned}

就有

f(x)=f1(x2)+xf2(x2).f(x)=f_1(x^2)+xf_2(x^2).

（注意这里 f1f_1 和 f2f_2 的系数是平方）

为了方便表示，令 WNk=x=e−i2πNkW_N^k=x=e^{-i\frac{2\pi}{N}k} ，可以发现

x2=e−i2πN2k=e−i2πN/2k=WN/2kf(WNk)=f1(WN/2k)+WNkf2(WN/2k).\begin{aligned} x^2=e^{-i\frac{2\pi}{N}2k}=e^{-i\frac{2\pi}{N/2}k}=W_{N/2}^k \\ f(W_N^k)=f1(W_{N/2}^k)+W_{N}^kf2(W_{N/2}^k). \end{aligned}

而我们知道美丽的欧拉公式 eiπ=−1e^{i\pi}=-1 ，就有

e−i2πN(k+N2)=e−i2πNk−iπ=−e−i2πNk.e^{-i\frac{2\pi}{N}(k+\frac{N}{2})}=e^{-i\frac{2\pi}{N}k-i\pi}=-e^{-i\frac{2\pi}{N}k}.

即

WNk+N2=−WNkWN/2k+N2=(WNk+N2)2=(−WNk)2=WN/2k.\begin{aligned} W_{N}^{k+\frac{N}{2}}=-W_{N}^k \\ W_{N/2}^{k+\frac{N}{2}}=(W_{N}^{k+\frac{N}{2}})^2=(-W_{N}^k)^2=W_{N/2}^k . \end{aligned}

那么

f(WNk+N2)=f1(WN/2k+N2)+WNk+N2f2(WN/2k+N2)=f1(WN/2k)−WNkf2(WN/2k).\begin{aligned} f(W_{N}^{k+\frac{N}{2}})=f_1(W_{N/2}^{k+\frac{N}{2}})+W_{N}^{k+\frac{N}{2}}f_2(W_{N/2}^{k+\frac{N}{2}}) \\ =f_1(W_{N/2}^k)-W_{N}^kf_2(W_{N/2}^k) . \end{aligned}

结合 f(WNk)f(W_N^k) 和 f(WNk+N2)f(W_{N}^{k+\frac{N}{2}}) 的计算公式，可以发现只需求出 f1(WN/2k)f_1(W_{N/2}^k) 和 f2(WN/2k)f_2(W_{N/2}^k) ，就可以同时得到这两者，而分别求 f1f_1 和 f2f_2 的问题规模都比直接求 f 要少一半。

注意，求单个 f1f_1 和 f2f_2 的值的时间复杂度仍然是 Θ(N)\Theta(N) ，但奇偶分治后，现在可以通过求两个值 f1f_1 和 f2f_2 而同时得到另外两个值 f(WNk)f(W_N^k) 和 f(WNk+N2)f(W_N^{k+\frac{N}{2}}) 。这意味着只要知道 k<N2k<\frac{N}{2} 的所有值，就可以得到剩余的 k>=N2k>=\frac{N}{2} 另一半值。

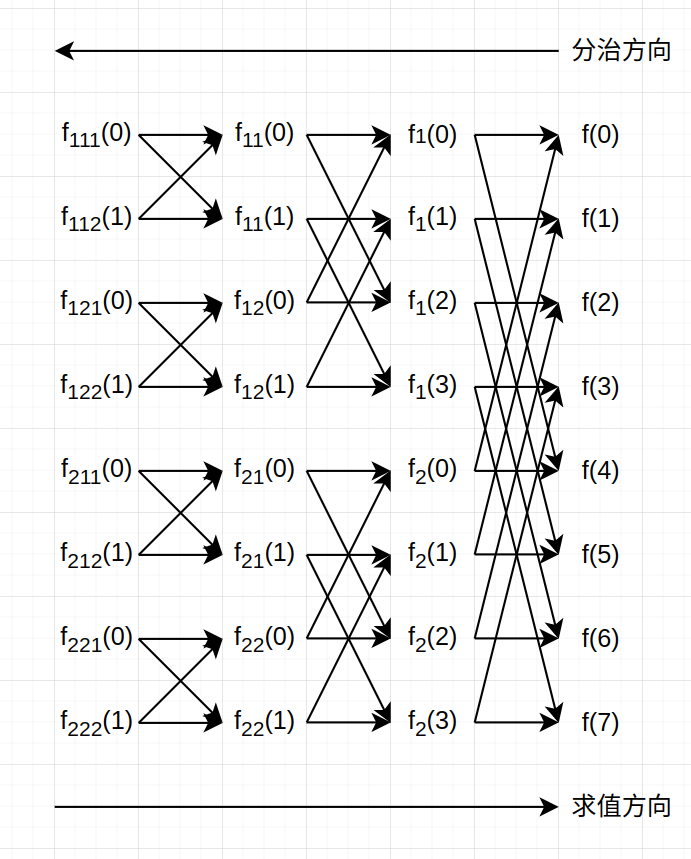
每次 N 减少一半，logN 次后 N 就将减少到 1 ，可以直接 O(1)O(1) 求出。因此整体的时间复杂度是 Θ(N+2×N2+4×N4+⋯+logN×1)=Θ(NlogN)\Theta(N+2\times\frac{N}{2}+4\times\frac{N}{4}+\cdots+logN\times1)=\Theta(NlogN) 。

许多读者可能仍然对分治的过程不太理解，不能想象为什么这样分治可以求出对于 k=0,1,⋯ ,N−1k=0, 1, \cdots, N-1 的所有值。所以我将画图来解释这个过程，以 N=8N=8 为例：

图中从右往左展示了每次奇偶分治的方向，而从左到右的箭头表示了数据产生的方向。可以看到，每个点的出边都有两条，表示一个 f1f_1 或 f2f_2 可以用于计算两个 ff 的值，而每个点的入边也有两条，表示每个 ff 都由一个 f1f_1 和一个 f2f_2 合并得到。这，就是蝶形变换。

至此，我们其实已经学会了 FFT 的原理，但此时的结论与实际所写的代码还有一些差别。由于递归分治的过程是很慢的，因此在实际编码中，往往使用迭代代替递归的方式。那么有什么办法能方便地把递归转化为迭代呢？

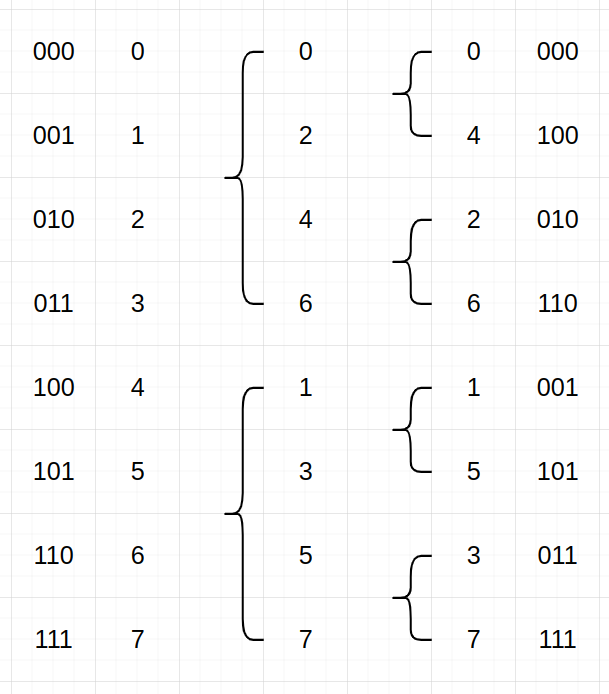
聪明的数学家们（或者计算机科学家们）再次找到了规律。让我们把奇偶分治的每一步画出来：

可以发现，分治的最底层的标号二进制位，恰好是原标号的二进制位的镜像！

因此只需倒置 0,1,⋯ ,N−10, 1, \cdots, N-1 的二进位，预处理好最底层的数的位置，然后按照蝶形变换的顺序依次进行合并就可以了。至于为什么会是这个巧妙的结果，应该不难证明，这里就不证了。

四、FFT的应用

FFT显然在信号与系统领域有极其广泛的应用，这里不再胡乱bb，只介绍在算法竞赛中的应用。

由于不管是离散信号，即数列，有在频率域下乘积等于时域下卷积的性质（当然连续信号也有），因此 FFT 在算法竞赛中最常见的考法就是题目要求以推公式也好、问题转化也好的各种方式，总之让你计算一个卷积表达式。朴素卷积计算是 O(N2)O(N^2) 的，而直接序列乘积的复杂度是 O(N)O(N) 的，因此先用 FFT 进行变换，序列乘积后再变换回去，就可以实现快速求卷积的效果。

FFT 一个最入门的应用是快速求高精度乘法，比如位数在 10610^6 位的两个数相乘，直接 N2N^2 乘肯定不行，万进制也不好使。而乘法其实就可以看成两个多项式的卷积。

令

A=a0+10a1+102a2+⋯+10N−1aN−1B=b0+10b1+102b2+⋯+10n−1bN−1.\begin{aligned} A=a_0+10a_1+10^2a_2+\cdots+10^{N-1}a_{N-1} \\ B=b_0+10b_1+10^2b_2+\cdots+10^{n-1}b_{N-1}. \end{aligned}

二者相乘的结果是

A×B=∑i=0N−1∑j=0N−1aibj10i+j.A\times B=\sum\limits_{i=0}^{N-1}\sum\limits_{j=0}^{N-1}{a_i}{b_j}10^{i+j}.

注意 10 的指数是与 i+ji+j 有关的，所以以 t=i+jt=i+j 为第一个求和的变量，得到

∑t=0N−1∑j=0tat−jbj10t=∑t=0N−110t∑j=0tat−jbj.\begin{aligned} \sum\limits_{t=0}^{N-1}\sum\limits_{j=0}^{t}{a_{t-j}}{b_{j}10^t} \\ =\sum\limits_{t=0}^{N-1}10^t\sum\limits_{j=0}^{t}{a_{t-j}}{b_{j}}. \end{aligned}

第二个求和部分其实就是卷积，而卷积的结果就是答案中的一个数位。卷积一次的复杂度是 O(N)O(N) 的，但是可以用 FFT 以 O(NlogN)O(NlogN) 的复杂度求出对于所有 tt 的卷积的值。

有同学可能会问，第二个求和的上限不是 tt 吗，还能直接先变换在序列乘吗？其实是可以的，只需把第二个求和的上限改为 N−1N-1 ，同时规定 ai=0 (i<0)a_i=0 \ (i<0) 就可以了。

FFT 求高精度乘的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int nn=310000;
struct cp{
    double r,i;
    cp(double _r=0,double _i=0):  r(_r),i(_i){}
    cp operator+(cp x){return cp(r+x.r,i+x.i);}
    cp operator-(cp x){return cp(r-x.r,i-x.i);}
    cp operator*(cp x){return cp(r*x.r-i*x.i,r*x.i+i*x.r);}
};
cp a[nn],b[nn],tmp[nn],_x,_y,c[nn];
char s1[nn],s2[nn];
int ans[nn],a1[nn],a2[nn],dig[nn];
int rvs[nn],N,L;
void fft(cp x[],int mk){
    for(int i=0;i<N;++i)  tmp[i]=x[rvs[i]];
    for(int i=0;i<N;++i)  x[i]=tmp[i];
    for(int i=2;i<=N;i<<=1){
        cp wn(cos(2*M_PI/i),mk*sin(2*M_PI/i));
        for(int k=0;k<N;k+=i){
            cp w(1,0);
            for(int j=k;j<k+i/2;++j){
                _x=x[j];  _y=x[j+i/2]*w;
                x[j]=_x+_y;  x[j+i/2]=_x-_y;
                w=w*wn;
            }
        }
    }
    if(mk==-1)  for(int i=0;i<N;++i)  x[i].r/=N;
}
int main(){
    scanf("%s%s",&s1,&s2);
    int l1=strlen(s1),l2=strlen(s2);
    for(N=1,L=0;N<max(l1,l2);N<<=1,++L);  N<<=1,++L;
    for(int i=0;i<N;++i){
        int l=0;
        for(int j=i;j;j>>=1)  dig[l++]=j&1;
        for(int j=0;j<L;++j)  rvs[i]=(rvs[i]<<1)|dig[j];
    }
    for(int i=0;i<l1;++i)  a1[l1-i-1]=s1[i]-'0';
    for(int i=0;i<l2;++i)  a2[l2-i-1]=s2[i]-'0';
    for(int i=0;i<N;++i)  a[i]=cp(a1[i]);
    for(int i=0;i<N;++i)  b[i]=cp(a2[i]);
    fft(a,1),fft(b,1);
    for(int i=0;i<N;++i)  c[i]=a[i]*b[i];
    fft(c,-1);
    for(int i=0;i<N;++i)  ans[i]=int(c[i].r+0.5);
    for(int i=0;i<N;++i)  ans[i+1]+=ans[i]/10,ans[i]%=10;
    int l=l1+l2-1;
    while(ans[l]==0 && l>0)  --l;
    for(int i=l;i>=0;--i)  printf("%d",ans[i]);
    cout<<endl;
    return 0;
}

这是高一时候写的代码，有些地方可能不太好看，不过 FFT 部分是抄网上的，已经非常成熟，可以直接拿去用。

除求高精度乘以外，还有一些不那么朴素的卷积题。

比如我非常喜欢的万径人踪灭，用卷积求回文子序列数，以及花样繁多的多项式计数题，这里限于个人能力就不一一介绍了。

五、总结

虽然 FFT 的原理实际上非常简单，但是我高中时期从未能静下心来深究过，而大学直到大三才发现，之前的理解一直都是错的（FFT 是整体加速，而不是对每一个卷积单独加速，之前一直理解错了）。这多亏了 shallow 问我 FFT 的问题，我才得以重新复习这个精彩的算法。这不禁让我想到了那句必背古诗：问渠哪得清如许，为有源头活水来。也希望看到这里的你能够真正理解蝴蝶变换的翅膀究竟是为谁扇动。